Maatriks on numbrite, sümbolite või avaldiste ristkülikukujuline paigutus ridades ja veergudes. Maatriksi korrutamiseks peate korrutama maatriksi esimese rea elemendid (või numbrid) maatriksi teise rea elementidega ja korrutama korrutise. Saate maatriksit korrutada vaid mõne lihtsa sammuga, mis nõuavad tulemuste õiget liitmist, korrutamist ja paigutamist.
Samm
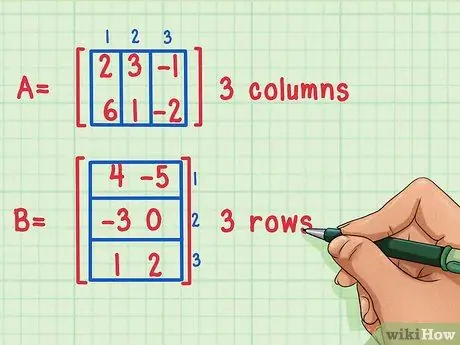
Samm 1. Veenduge, et maatriksid on korrutatavad
Maatriksit saab korrutada ainult siis, kui esimese maatriksi veergude arv on võrdne teise maatriksi ridade arvuga.
Neid maatrikseid saab korrutada, sest esimesel maatriksil, maatriksil A, on 3 veergu, teisel maatriksil maatriks B aga 3 rida
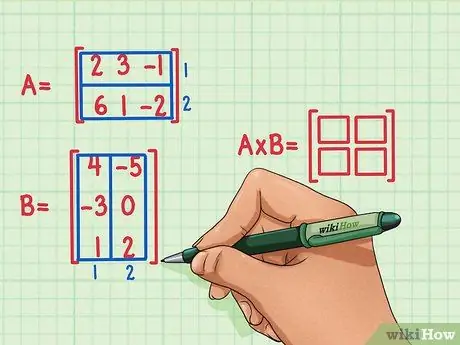
Samm 2. Märkige maatrikstoote mõõtmed
Looge uus tühi maatriks, mis märgib kahe maatriksi korrutise korrutised. Maatriksil, mis tähistab maatriksi A ja maatriksi B korrutist, on sama rida kui esimesel maatriksil ja sama palju veerge kui teisel maatriksil. Selle maatriksi ridade ja veergude arvu kuvamiseks võite joonistada tühjad kastid.
- Maatriksil A on 2 rida, seega on maatriksi korrutamise tulemusel 2 rida.
- Maatriksil B on 2 veergu, seega on maatriksi korrutamise tulemusel 2 veergu.
- Maatrikstoote tulemuseks on 2 rida ja 2 veergu.
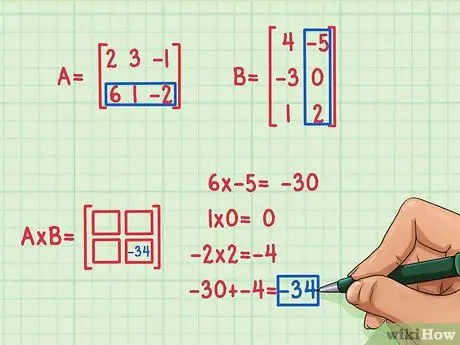
Samm 3. Leidke esimese täpptoote tulemus
Esimese punkttoote tulemuse leidmiseks peate korrutama esimese rea esimese elemendi esimese veeru esimese elemendiga, esimese rea teise elemendi esimese veeru teise elemendiga ja kolmanda elemendi esimene rida esimese veeru kolmanda elemendi võrra. Seejärel lisage leidmiseks korrutamistulemused täpptoode (punkt).
Oletame, et olete otsustanud kõigepealt arvutada maatrikstoote teise rea ja teise veeru (paremal all) elemendid. Seda saate teha järgmiselt.
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Punkttoote tulemus on -34 ja see tulemus kirjutatakse maatriksprodukti paremasse alumisse serva.
Maatriksi korrutamisel kirjutatakse punkttoode esimese maatriksi rea ja teise maatriksi veeru positsiooni. Näiteks kui teate maatriksi A alumise rea ja maatriksi B parema veeru punkttooteid, kirjutatakse vastus -34 maatrikstoote alumisse ja paremasse veergu
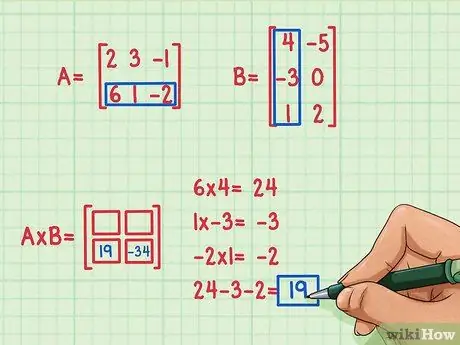
Samm 4. Leidke teise punkti toote tulemus
Oletame, et soovite leida termini maatrikstoote vasakus alanurgas. Selle termini leidmiseks peate lihtsalt korrutama esimese maatriksi alumise rea elemendid teise maatriksi esimese veeru elementidega ja seejärel need kokku liitma. Kasutage sama meetodit kui esimese rea ja veeru korrutamine - otsige uuesti täpne toode (ära tee)tema oma.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Punkttoote tulemus on -19 ja see tulemus kirjutatakse maatriksprodukti vasakus alanurgas.
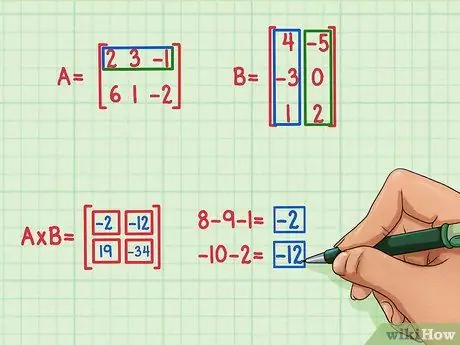
Samm 5. Leidke ülejäänud kaks punkti
Termini leidmiseks maatrikstoote vasakus ülanurgas leidke kõigepealt maatriksi A ülemise rea ja maatriksi B vasaku veeru punkttoode. Siin on, kuidas seda teha.
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Punkttoote tulemus on -2 ja see tulemus kirjutatakse maatriksprodukti vasakus ülanurgas.
Termini leidmiseks maatrikstoote paremas ülanurgas otsige lihtsalt maatriksi A ülemise rea ja maatriksi B parema veeru punkttooteid. Seda saate teha järgmiselt
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Punkttoode on -12 ja see tulemus on kirjutatud maatriksprodukti paremas ülanurgas.
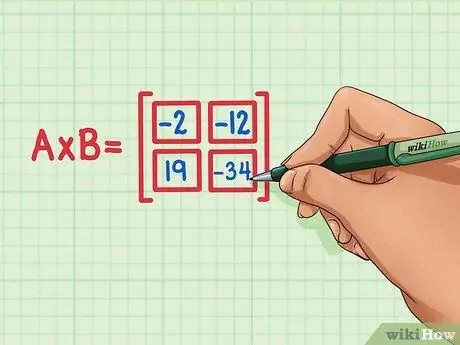
Samm 6. Veenduge, et neli punktiga tooted oleksid maatrikstoote õiges kohas
19 peab olema all vasakul, -34 peab olema all paremal, -2 peab olema üleval vasakul ja -12 peab olema üleval paremal.
Näpunäiteid
- Joonelõigete kasutamine ja mitte joonte kasutamine võib anda vale vastuse. Kui rida tähistav joon nõuab veeru ületamiseks pikendust, siis pikendage seda! See on vaid visualiseerimistehnika, mis võimaldab teil hõlpsamini teada, milliseid ridu ja veerge toote iga elemendiga töötamiseks kasutada.
- Kahe maatriksi korrutis annab ridade arvu, mis on võrdne esimese maatriksi ridade arvuga, ja veergude arv võrdub teise maatriksi veergude arvuga.
- Kirjutage oma summa üles. Maatriksite korrutamine hõlmab palju arvutusi ja on väga lihtne kõrvale kalduda ja unustada, millist arvu korrutate.
