Kümnendarv (põhikümnes) on iga numbri kohta kümne võimaliku väärtusega (0, 1, 2, 3, 4, 5, 6, 7, 8 või 9). Seevastu binaarsel (teise aluse) arvusüsteemil on iga numbri positsiooni jaoks ainult kaks võimalikku väärtust, mida tähistavad 0 ja 1. Kuna binaararvude süsteem on elektrooniliste arvutite sisekeel, teavad tõsised arvutiprogrammeerijad, kuidas teisendada kümnendarvust binaarsüsteemiks. Järgige neid lihtsaid samme ja ka seda, kuidas seda konversiooni juhtida.
Samm
Meetod 1: 2: lühike jagamine kahega jäägiga
Samm 1. Määrake probleem
Selle näite puhul teisendame kümnendarvu 15610 olla kahendarv. Kirjutage jagatud arvuks kümnendarv ümberpööratud jagamise sümbolisse. Kirjutage jaotussümboli kõverast väljas jagajaks sihtkoha numbrisüsteemi alus (selles näites “2” binaarse jaoks).
- Seda meetodit on paberile joonistades palju lihtsam mõista ja algajatel palju lihtsam, sest see jagab ainult kahega.
- Segaduste vältimiseks enne ja pärast teisendamist kirjutage arvutatava numbrisüsteemi põhinumber alamindeksina (väiketähed, mis on eraldusmärgina kirjutatud tavaliste tähtede all). Selles näites on kümnendnumbri alamindeks 10 ja binaararv 2.
Samm 2. Tehke jagamine
Kirjutage täisjaotus (jagatis) pika jagamise sümboli alla ja ülejäänud (0 või 1) jagatud numbrist paremale.
Kuna me jagame kahega, kui jagatav arv on paarisarv, on jääk 0 ja kui jagatav arv on paaritu arv, siis ülejäänud on 1
Samm 3. Jätkake jagamist, kuni see jõuab nulli
Jätkake allamäge, jagades iga uue jagatise kahega ja kirjutades ülejäänud osa igast jagatud numbrist paremale. Peatage, kui jagatis on null.
Samm 4. Kirjutage üles uus kahendarv
Alustades madalaimast allesjäänud numbrist, lugege ülejäänud järjekorda kasvavas järjekorras ülespoole. Selle näite puhul peaksite saama tulemuse 10011100. See on kümnendarvu 156. binaarne ekvivalent. Või kui see on kirjutatud numbrilise baasindeksiga: 15610 = 100111002.
Seda meetodit saab muuta, et teisendada kümnendbaasist mis tahes numbribaasiks. Jagaja on 2, sest sihtkoha numbrisüsteemi alus on baas 2 (binaarne). Kui sihtkoha numbrisüsteemi alus on teine baas, asendage selle meetodi baasnumber sobiva baasinumbriga. Näiteks kui sihtkoha baas on baas 9, asendage baasi 2 number numbriga 9. Lõpptulemus saab otse sihtbaasi numbri kujul
Meetod 2/2: kahe tuletamine ja lahutamine
Samm 1. Alustage tabeli loomisega
Kirjutage kahe tabelinumbri võimsused "tabeli 2 alusele" paremalt vasakule. Alusta kell 20, kirjutage see "1". Tõstke auastet iga auastme kohta 1 võrra. Täitke tabelit, kuni saate numbri, mis on kõige lähemal arvutatava kümnendsüsteemi arvule. Selle näite puhul teisendame kümnendarvu 15610 olla kahendarv.
Samm 2. Leidke põhinumbri 2 suurima võimsusega number
Valige tabelist suurim arv, mis on teisendatavaga võrdne või väiksem. Number 128 on põhinumbri 2 suurima võimsusega number ja on ka väiksem kui 156, seega kirjutage tabeli selle lahtri alla number "1", kus tabeli suurim arv asub vasakul (vt tabelit ülaltoodud pildil). Seejärel lahutage algarvust 128, saate: 156 - 128 = 28.
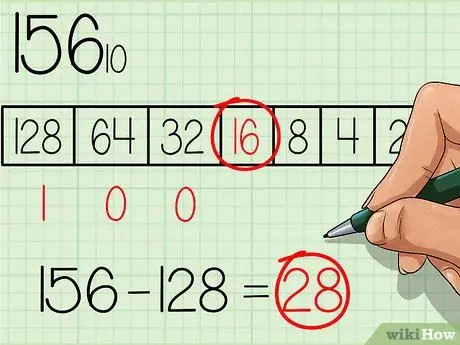
Samm 3. Jätkake järgmise väiksema võimsusega tabelis
Uue numbri (28) abil jätkake tabeli läbimist vasakult paremale, kontrollides samal ajal, kas numbrid on uue numbriga võrdsed või väiksemad. Number 64 ei ole väiksem kui 28, seega kirjutage numbrikasti 64 alla number „0”. Jätkake, kuni leiate numbri, mis on võrdne või väiksem kui 28.
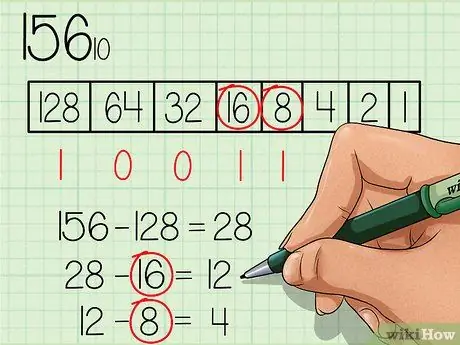
Samm 4. Lahutage pidevalt igast arvust, mis on võrdne või väiksem uuest numbrist, ja märkige sobiva numbri kasti alla number “1”
Arv 16 on väiksem kui 28, seega kirjutage numbrikasti 16 alla number 1 ja lahutage 16 28 -st, nii saate uue numbri 12. Number 8 on väiksem kui 12, seega kirjutage number "1" alla numbrikast 8 ja lahutage 8 12 -st, et saada uus number 4.
Samm 5. Jätkake, kuni jõuate tabeli lõppu
Ärge unustage märkida iga kasti alla “1”, kui numbrid on võrdsed või väiksemad kui uus number, ja “0” iga kasti all, kui numbrid on endiselt suuremad kui uus number.
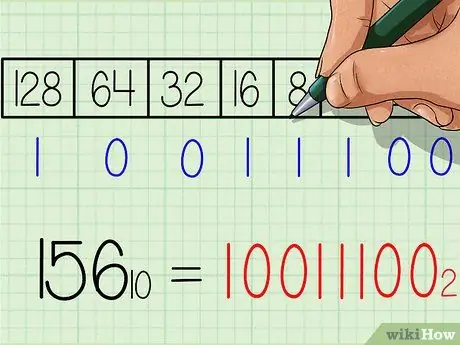
Samm 6. Kirjutage binaararvu vastus üles
Arv on vasakult paremale täpselt sama, mis tabeli allosas olev numbririda „1” ja „0”. Peaksite saama tulemuse 10011100. See on kümnendarvu 156. binaarne ekvivalent. Või kui see on kirjutatud allindeksiga: 15610 = 100111002.
Selle meetodi kordamine aitab teil mäletada baasi teise võimeid, nii et saate 1. sammu vahele jätta
Näpunäiteid
- Operatsioonisüsteemi sisseehitatud kalkulaatoriprogramm saab selle konversiooni teie eest teha, kuid programmeerijana on kõige parem alustada konversioonide toimimise mõistmisest. Kalkulaatori programmi teisendusvalikuid saab nähtavaks teha, avades menüü „Vaade” ja valides „Programmeerija” (Windows 7 ja 8 jaoks).
- Vastupidises suunas teisendamist, s.o binaar- ja kümnendarvude süsteemi, on tavaliselt kõigepealt lihtsam õppida.
- Sageli harjutage kümnendarvude teisendamist binaarseks, et saada asjatundlikumaks.
