- Autor Jason Gerald [email protected].
- Public 2024-01-16 19:23.
- Viimati modifitseeritud 2025-01-23 12:16.
Kiirus on arvutus selle kohta, kui kiiresti miski korraga liigub. Kui olete kunagi vaadanud liikuva auto spidomeetrit, näete kiiruste arvu - mida kaugemale nõel liigub, seda suurem on sõiduki kiirus. Sõltuvalt teie teabe tüübist on kiiruse arvutamiseks mitmeid viise. Üldiselt valem kiirus = vahemaa/aeg (või k = j/w) on lihtsaim viis kiiruse arvutamiseks.
Samm
Meetod 1 /3: standardkiiruse arvutamise valemite kasutamine

Samm 1. Leidke objekti läbitud vahemaa
Põhivalemit, mida enamik inimesi kasutab millegi kiiruse leidmiseks, on väga lihtne kasutada. Kõigepealt peate teadma, "kui palju on mõõdetud objekt läbinud". Teisisõnu, kui suur on kaugus objekti algus- ja lõpp -punkti vahel?
Seda valemit on näite abil lihtsam mõista. Oletame, et sõidame autoga 161 kilomeetri pikkusele mänguväljakule. Mõne sammuga saame seda teavet kasutada valemi arvutamise lõpuleviimiseks

Samm 2. Leidke aeg, mis kulub objektil selle vahemaa läbimiseks
Järgmine vajalik teave on see, kui kaua kulub objektil teatud kaugusele jõudmiseks. Teisisõnu, kui kaua võtab aega, kuni objekt liigub alguspunktist lõpp -punkti?
Selles näites oletame, et objekt võtab u. kaks tundi sihtkohta jõudmiseks.

Samm 3. Jagage kaugus objekti kiiruse leidmiseks kulunud ajaga
Objekti kiiruse teadmiseks vajate ainult neid kahte teavet. Kaugus ajast on võrdne objekti kiirusega.
Selles näites 161 kilomeetrit/2 tundi = 80,5 kilomeetrit tunnis.

Samm 4. Ärge unustage kasutatud seadet
On väga oluline kasutada vastuses õigeid ühikuid (näiteks kilomeetreid tunnis jne) Ilma nende üksusteta on inimestel väga raske mõista teie vastuse tähendust. Samuti võite punkte kaotada, kui kasutate koolist ülesannete täitmisel vale ühikut.
Kiiruse ühik on kaugusühik ajaühikuni. Näiteks kuna me mõõdame kaugust kilomeetrites ja aega tundides, on kasutatud ühikud kilomeetrit/tund (või kilomeetrit tunnis).
Meetod 2/3: keerulisemate arvutuste lahendamine

Samm 1. Leidke kauguse ja aja probleemi lahendamiseks mitu erinevat muutujat
Kui olete kiiruse põhivalemist aru saanud, saate seda kasutada muude arvutuste tegemiseks kui kiirus. Näiteks kui teate alguses ainult objekti kiirust ja veel üht muutujat, saate tundmatu teabe leidmiseks ülaltoodud valemi ümber korraldada.
-
Oletame näiteks, et me teame, et rong sõidab neli tundi kiirusega 20 kilomeetrit tunnis, kuid me ei tea, kui kaugele ta on sõitnud. Selle selgitamiseks saame valemi ümber korraldada järgmiselt.
-
- kiirus = vahemaa/aeg
- kiirus × aeg = (vahemaa/aeg) × aeg
- kiirus × aeg = vahemaa
- 20 km/tund × 4 tundi = vahemaa = 80 kilomeetrit
-

Samm 2. Vajadusel teisendage kasutatavad ühikud
Mõnikord võite kiirust arvutada teatud ühiku abil, kuid peate selle teisendama teiseks ühikuks. Sellisel juhul peate kasutama teisendustegurit, et saada vastus õigete ühikute järgi. Selleks kirjutage lihtsalt ühikute suhe murdosa kujul ja korrutage. Korrutades pöörake murdosa soovimatute ühikute eemaldamiseks ümber. See meetod on palju lihtsam kui tundub!
-
Oletame näiteks, et ülaltoodud näiteülesandes vajame vastust kilomeetrite asemel miilides. Üks miil võrdub umbes 1,6 kilomeetriga. Niisiis, saame teisendada järgmiselt:
-
- 80 kilomeetrit × 1 miil/1,6 kilomeetrit = 50 miili
-
- Pidage meeles, et kuna murdosa lõpus kuvatakse kilomeetreid, eemaldab see eelmisest vastusest kilomeetrid, seega kasutab lõpptulemus miile.
- See veebisait pakub enamiku enamkasutatavate üksuste teisendusfunktsioone.

Samm 3. Vajadusel asendage muutuja "distance" kaugusvalemiga
Objektid ei liigu alati sirgel ja sujuval teel. Kui see on tõsi, ei pruugi te tavalise kiiruse valemisse sisestada lihtsalt kaugusühikuna arvväärtust. Siiski peate võib -olla asendama tähe j valemis k = j/w valemiga, mis sarnaneb objekti läbitud vahemaaga.
-
Oletame näiteks, et lennuk pöörleb läbi õhu 20 miili kaugusel 5 korda. Lennuk läbis ringi poole tunniga. Selles näites peame enne selle kiiruse määramist leidma lennuki läbitud kogupikkuse. Selles valemis saame kasutada j -i asemel kaugust ringjoone (selle ümber) arvutamiseks valemit. See valem on ümbermõõt = 2πr, kus r = ringi raadius. Selle lahendamiseks toimige järgmiselt.
-
- k = (2 × × r)/mass
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 miili tunnis
-

Samm 4. Mõista, et k = j/w annab keskmise kiiruse
Lihtne ja lihtne valem, mida kasutame kiiruse leidmiseks, on üks puudus. Saadud väärtus on tehniliselt keskmine kiirus. See tähendab, et valem eeldab, et teie mõõdetav objekt kasutab liikumisel sama kiirust. Nagu allpool näeme, on objekti kiiruse leidmine ühe hetkega palju keerulisem.
Selle erinevuse näitlikustamiseks kujutage ette viimast korda autoga reisimist. On ebatõenäoline, et reisite sama kiirusega kui reisite. Tavaliselt alustate teekonda siiski väikese kiirusega ja suurendate järk -järgult kiirust, peatudes punaste tulede, ummikute jms tõttu. Kui kasutate kiiruse leidmiseks sõidu ajal standardkiiruse valemit, ei saa selle kiiruse muutusi tuvastada. Küll aga saate vastuse, mis näitab kõigi sõidetud kiiruse erinevuste keskmist kiirust
3. meetod 3 -st: kiiruse arvutamine
Märge:
Selles jaotises kasutatakse tehnikaid, mis on vähem tuttavad inimestele, kes pole kunagi arvutust õppinud. Abi saamiseks lugege meie artikleid arvutuste kohta.
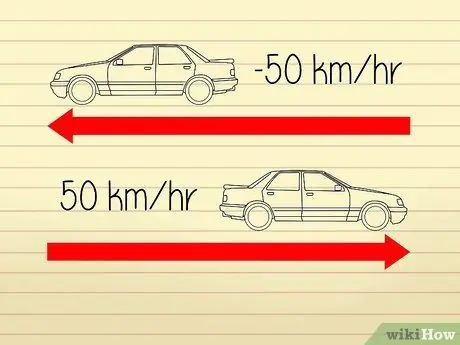
Samm 1. Mõista, et kiirus on määratletud kui kiirenduskiirus
Kõrgetasemelised kiiruse arvutused on üsna segased, sest matemaatikud ja teadlased kasutavad "kiiruse" ja "kiirenduse" kirjeldamiseks erinevaid määratlusi. Kiirendusel on kaks komponenti: "kiirus" ja "suund". Kiirus võrdub objekti kiirusega. Suuna muutmine põhjustab muutusi kiirenduses, kuid mitte kiirust.
- Oletame näiteks, et kaks autot liiguvad vastassuunas. Mõlema auto kiirusmõõturid näitavad kiirust 50 km/h, nii et mõlemad sõidavad sama kiirusega. Kuna aga autod liiguvad üksteisest eemale, võime öelda, et ühel autol on kiirendus -50 km/h, teisel aga 50 km/h.
- Nii nagu hetkelise kiiruse arvutused, saate teha ka hetkelise kiirenduse arvutusi.

Samm 2. Negatiivse kiirenduse mõõtmiseks kasutage absoluutväärtusi
Objektil võib olla negatiivne kiirendus (kui see liigub teise objekti suhtes negatiivses suunas). Siiski ei ole negatiivset kiirust. Niisiis, sel juhul näitab kiiruse absoluutväärtus objekti kiirust.
Sel põhjusel on ülaltoodud näiteülesandes mõlemal autol kiirus 50 km/h.
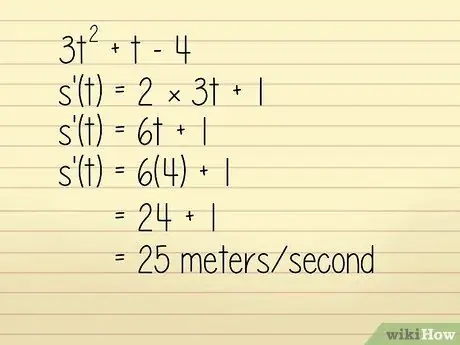
Samm 3. Võtke funktsiooni positsiooni tuletis
Kui teil on funktsioon k (w), mis näitab objekti asukohta ilma aega arvutamata, näitab k (w) tuletis kiirendust ilma ajastuseta. Lihtsalt ühendage ajaväärtus selle valemiga, nii et muutuja w (või mis iganes ajaväärtust kasutatakse) kiireneks vastavalt sellele ajale. Siit saate hõlpsalt leida objekti kiiruse.
-
Oletame näiteks, et objekti asukohta ühes meetris kirjeldatakse võrrandis 3q2 + w - 4 kus w = aeg sekundites. Tahame teada objekti kiirust w = 4 sekundit. Sel juhul saate selle lahendada järgmiselt.
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Nüüd sisestame w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 meetrit sekundis. Tehniliselt on see kiirenduse arvutamine, kuid kuna see on positiivne ja suunda küsimuses ei mainita, saame seda kasutada kiiruse leidmiseks.
-

Samm 4. Võtke integreeritud kiirendusfunktsioon
Kiirendus on viis objekti kiirenduse muutuse mõõtmiseks aja jooksul. See teema on liiga keeruline, et seda selles artiklis täielikult selgitada. Siiski on kasulik märkida, et kui teil on funktsioon a (w), mis tähistab kiirendust aja suhtes, tagastab a (w) integraal selle aja põhjal kiirenduse tulemuse. Pidage meeles, et on väga kasulik teada objekti esialgset kiirendust, et saaksite selle tulemuse konstandi lõpmatust integraalist määratleda.
-
Oletame näiteks, et objektil on pidev kiirendus (m/s2 tulemusena (w) = -30. Ütle ka, et objekti algkiirendus on 10 m/s. Peame leidma kiiruse w = 12 sekundit. Sel juhul saame selle lahendada järgmiselt:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
C leidmiseks lahendame p (w), kui w = 0. Pidage meeles, et objekti algkiirendus on 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, seega p (w) = -30w + 10
-
-
Nüüd saame sisestada w = 12 sekundit.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Kuna kiirus on kiirenduse absoluutväärtus, on objekti kiirus 350 meetrit sekundis.
-
Näpunäiteid
- Harjutamine teeb suurepäraseks! Proovige luua oma küsimus, asendades ülaltoodud näiteülesande numbrid.
- Kui otsite kiiret viisi arvutamise harjutamiseks parema arvutamiskiiruse saavutamiseks, kasutage siin olevat tuletisinstrumentide kalkulaatorit ja siinset integraalkalkulaatorit.






