Kuidas arvutada objektiivi suurendust: 12 sammu (piltidega)

2024 Autor: Jason Gerald | [email protected]. Viimati modifitseeritud: 2024-01-16 19:23

Optiliste instrumentide uurimisel on läätsetaolise objekti "suurenduseks" nähtuva pildi kõrguse ja objekti tegeliku kõrguse suhe. Näiteks objektiivil, mis võib objekti väga suurena välja näha, on "kõrge" suurendustegur, samas kui objektiivil, mis muudab objekti väikese välimusega, on "madal" suurendustegur. Objekti suurendamise valem arvutatakse tavaliselt valemi abil M = (h_i/h_o) = -(d_i/d_o), kus M = suurendus, h_i = pildi kõrgus, h_o = objekti kõrgus ja d_i ja D_o = pildi ja objekti kaugus.

Samm

Meetod 1: 2: ühe objektiivi suurenduse arvutamine

Märkused: A koonduv lääts keskelt laiem kui äärtest (nagu suurendusklaas). a lahknev objektiiv äärtest laiem kui keskel (nagu kauss). Mõlema objektiivi suurenduse arvutamine on sama üks oluline erand. Klõpsake siin, et minna otse erinevate läätsede erandite juurde.

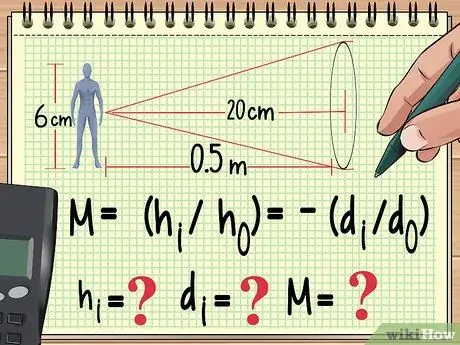
Samm 1. Alustage oma võrrandist ja juba tuttavatest muutujatest

Nagu iga teine füüsikaprobleem, on laienemisülesande lahendamise viis üles kirjutada võrrand, mida selle arvutamiseks kasutate. Siit saate töötada tagasi, et leida selle muutuja väärtus, mida te pole võrrandist leidnud.

Oletame näiteks, et 6 cm kõrgune nukk asetatakse ühe meetri kaugusele a koonduv lääts fookuskaugusega 20 cm. Kui tahame arvutada suurendust, pildi kõrgust ja pildi kaugust, võime hakata oma võrrandit kirjutama järgmiselt.

M = (h_i/h_o) = -(d_i/d_o)
Nüüd teame h_o (nuku kõrgus) ja d_o (nuku kaugus objektiivist). Teame ka objektiivi fookuskaugust, mida selles võrrandis pole. Me loeme h_i, d_ija M.

Samm 2. Kasutades läätse võrrandit d saamiseks_i.

Kui teate kaugust suurendatavast objektist ja objektiivi fookuskaugust, on kauguse arvutamine moodustatud pildist objektiivi võrrandiga väga lihtne. Objektiivi võrrand on 1/f = 1/päev_o + 1/päev_i, kus f = läätse fookuskaugus.

Selle näiteülesande puhul saame objektiivi võrrandit kasutada d arvutamiseks_i. Sisestage väärtused f ja d_i siis lahendage võrrand:

1/f = 1/päev_o + 1/päev_i

1/20 = 1/50 + 1/päev_i

5/100 - 2/100 = 1/päev_i

3/100 = 1/päev_i

100/3 = d_i = 33,3 cm
Objektiivi fookuskaugus on kaugus objektiivi keskpunktist kuni fookuspunktis valguse edastamise punktini. Kui olete kunagi fokuseerinud valgust suurendusklaasiga põletavatele sipelgatele, olete seda näinud. Tunni küsimustes on tavaliselt antud selle leviala suurusjärk. Reaalses elus on need spetsifikatsioonid tavaliselt kirjutatud objektiivil asuvale sildile.

Samm 3. Arvutamine h_i.

Pärast arvutamist d_o ja D_i, saate arvutada suurendatud objekti kõrgust ja objektiivi suurendust. Pange tähele kahte võrdusmärki läätse suurendusvõrrandis (M = (h_i/h_o) = -(d_i/d_o)) - see tähendab, et kõik selle võrrandi osad on üksteisega võrdsed, nii et saame arvutada M ja h_i mis tahes järjekorras me tahame.

Selle näiteülesande jaoks saame arvutada h_i nagu nii:

(h_i/h_o) = -(d_i/d_o)

(h_i/6) = -(33, 3/50)

h_i = -(33, 3/50) x 6

h_i = - 3, 996 cm
Pange tähele, et objekti kõrgus on siin negatiivne, mis näitab, et pilt, mida me hiljem näeme, pööratakse ümber (ülevalt alla).

Samm 4. M. arvutamine

Viimase muutuja saate arvutada võrrandiga -(d_i/d_o) või (h_i/h_o).

Järgmises näites on M arvutamine järgmine:

M = (h_i/h_o)

M = (-3, 996/6) = - 0, 666
Tulemus on sama ka siis, kui see arvutatakse väärtuse d abil:

M = -(d_i/d_o)

M = -(33, 3/50) = - 0, 666
Pange tähele, et suumil pole ühiku silti.

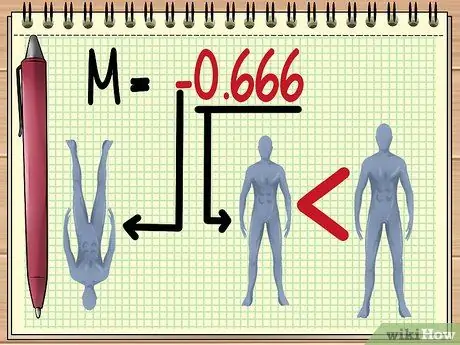
Samm 5. M väärtuse mõistmine

Kui olete saanud M väärtuse suuruse, saate objektiivi kaudu nähtava pildi kohta hinnata mitmeid asju, nimelt:

Suurus.

Mida suurem on M "absoluutväärtus", seda suurem on objektiiv, mida objektiiviga vaadatakse. M väärtus vahemikus 0 kuni 1 näitab, et objekt näeb välja väiksem.
Objekti orientatsioon.

Negatiivne väärtus näitab, et moodustatud pilt pööratakse ümber.
Siin toodud näites tähendab M väärtus -0,666, et vastavalt olemasoleva muutuja väärtusele on nuku vari nähtav. tagurpidi ja kaks kolmandikku väiksem kui tegelik suurus.

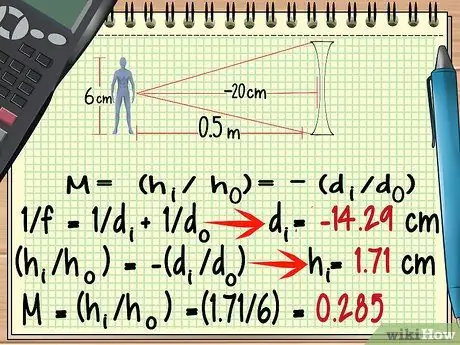
Samm 6. Erineva objektiivi puhul kasutage negatiivset fookuspunkti

Kuigi erineva läätse kuju erineb suuresti koonduva objektiivi kujust, saate selle suurenduse arvutada sama valemi abil, nagu eespool. Erandid, mida meeles pidada, on Erineva objektiivi fookuspunkt on negatiivne.

Ülaltoodud näiteülesandes mõjutab see vastust, mille saate d arvutamisel_i, seega pöörake sellele kindlasti tähelepanu.

Töötleme ülaltoodud näiteprobleemi ümber, alles nüüd kasutame fookuskaugusega erinevat objektiivi - 20 cm.

Ülejäänud muutujad jäävad samaks.
Kõigepealt arvutame d_i kasutades läätse võrrandit:

1/f = 1/päev_o + 1/päev_i

1/-20 = 1/50 + 1/päev_i

-5/100 - 2/100 = 1/päev_i

-7/100 = 1/päev_i

-100/7 = d_i = - 14, 29 cm
Nüüd arvutame h_i ja M väärtusega d_i uus.

(h_i/h_o) = -(d_i/d_o)

(h_i/6) = -(-14, 29/50)

h_i = -(-14, 29/50) x 6

h_i = 1, 71 cm

M = (h_i/h_o)

M = (1, 71/6) = 0, 285

Meetod 2/2: mitme objektiivi suurenduse arvutamine

Lihtne kahe objektiivi meetod

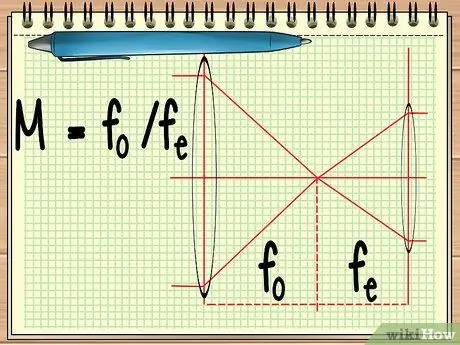
Samm 1. Arvutage kahe läätse fookuspunkt

Kui kasutate instrumenti, mis koosneb kahest kõrvuti asetatud läätsest (näiteks teleskoop või binokkel), peate välja selgitama vaid kahe läätse fookuspunkti, et arvutada kahe läätse üldine suurendus. seda saab arvutada lihtsa võrrandi abil M = f_o/f_e.

Võrrandis on f_o on objektiivi fookuspunkt ja f_e on okulaari fookuspunkt. Objektiiv on suur objektiiv, mis asub objekti lähedal, samas kui silma lääts on lääts, mis asub vaatleja silma lähedal.

Samm 2. Ühendage juba olemasolev teave võrrandiga M = f_o/f_e.

Kui teil on mõlema läätse fookuspunktid, on neid väga lihtne arvutada, - arvutage suhe, jagades objektiivi fookuskauguse okulaari fookuskaugusega. Vastuseks saate tööriista täieliku suurenduse.

Oletame näiteks lihtsat teleskoopi, kirjutatakse, et objektiivi fookuspunkt on 10 cm ja okulaari fookuspunkt 5 cm, siis on suurendus 10/5 = 2.

Keeruline meetod

Samm 1. Arvutage läätsede ja objekti vaheline kaugus

Kui teil on objektiivi ette paigutatud kaks objektiivi, saab kogu suurenduse arvutada, kui teate kaugust läätsedest objektini, objekti suurust ja kahe objektiivi fookuspunkti. Ülejäänud saab ka arvutada.

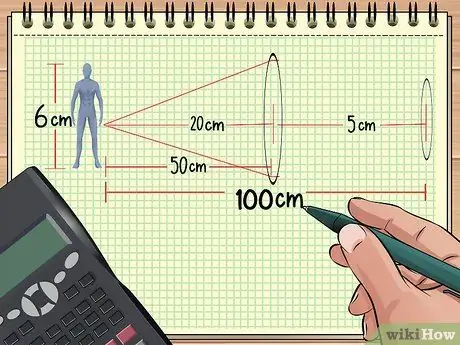
Oletame näiteks, et me paigutame esemed ja läätsed nii, nagu ülaltoodud näiteülesandes 1: nukk on 50 cm kaugusel koonduvast läätsest, mille fookuskaugus on 20 cm. Nüüd asetage teine lääts fookuspunktiga 5 cm esimesest läätsest 50 cm kaugusele (nukust 100 cm kaugusele.) Pärast seda arvutame saadud suurenduse põhjal kogu suurenduse

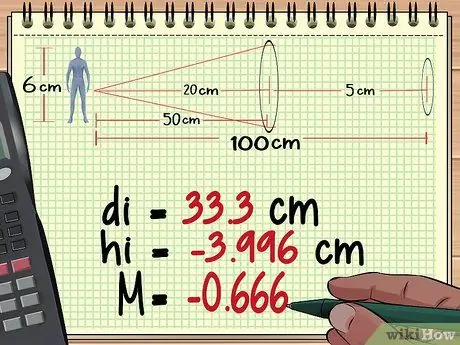
Samm 2. Arvutage objektiivi 1 kaugus, kõrgus ja suurendus

Mitme läätse suurenduse arvutamise esimene osa on sama, mis ühe objektiivi suurenduse arvutamine. Alustage objektile lähimast objektiivist, kasutage objektiivi võrrandit, et leida kaugus moodustatud pildist, seejärel kasutage suurenduse võrrandit pildi kõrguse ja suurenduse leidmiseks. Üksikute objektiivide suurendusarvutuste vaatamiseks klõpsake siin.

Ülaltoodud meetodi 1 arvutuste põhjal leiame, et esimene objektiiv toodab nii kõrge pildi - 3, 996 cm, kaugus Pikkus 33,3 cm objektiivi taga ja suurendusega - 0, 666.

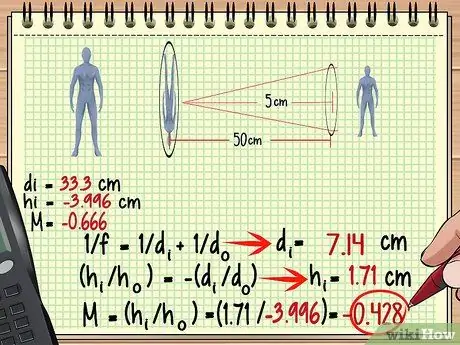
Samm 3. Kasutage esimese objektiivi pilti teise objektiivi objektina

Nüüd on teise objektiivi suurenduse, kõrguse ja muu leidmine väga lihtne - kasutage sama meetodit, mida kasutasite esimese objektiivi puhul, ainult seekord käsitlege pilti objektina. Pidage meeles, et pildi kaugus teisest objektiivist ei ole alati sama kui objekti kaugus esimesest objektiivist.

Ülaltoodud näites, kuna pilt moodustub esimese objektiivi taga 33,3 cm, on vahemaa 50-33,3 = 16,7 cm teise objektiivi ees. Kasutame seda mõõtmist ja teise objektiivi fookuskaugust, et leida teise objektiivi moodustatud pilt.

1/f = 1/päev_o + 1/päev_i

1/5 = 1/16, 7 + 1/päev_i

0, 2 - 0, 0599 = 1/päev_i

0, 14 = 1/päev_i

d_i = 7, 14 cm
Nüüd saame arvutada h_i ja M teise objektiivi puhul:

(h_i/h_o) = -(d_i/d_o)

(h_i/-3, 996) = -(7, 14/16, 7)

h_i = -(0, 427) x -3, 996

h_i = 1, 71 cm

M = (h_i/h_o)

M = (1, 71/-3, 996) = - 0, 428

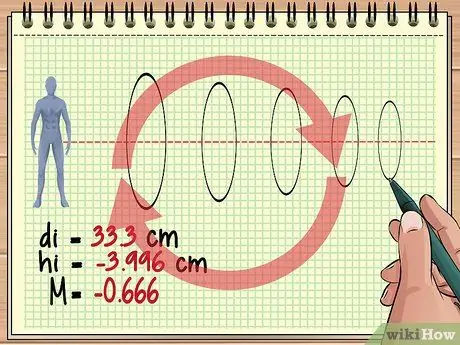
Samm 4. Jätkake täiendavate läätsede arvutamist

See põhiline lähenemisviis on sama, kui objekti ette on paigutatud kolm, neli või sada objektiivi. Arvestage iga objektiivi puhul objektiivina eelmise objektiivi pilti ning kasutage soovitud vastuse leidmiseks läätse võrrandit ja suurendusvõrrandit.

Pidage meeles, et iga järgmine objektiiv võib tekkinud kujutist pidevalt ümber pöörata. Näiteks näitab varasem suurendusväärtus (-0, 428), et pilt, mida me vaatame, on ligikaudu 4/10 tegelikust objekti suurusest, kuid risti, kuna eelmise objektiivi pilt on ümberpööratud

Näpunäiteid

Binokkel annab tavaliselt selgituse suurenduse spetsifikatsioonide kohta arvuga, mis on kordne teise numbriga. Näiteks saab binokli määrata 8x25 või 8x40. Niimoodi kirjutades on esimene number binokli suurendus. Pole tähtis, isegi kui antud näites on need kaks suurust erinevad, mõlemal binokkel on suurendus 8 korda. Teine number näitab, kui selge pildi binokkel moodustab.
Pidage meeles, et ühe objektiiviga luupide puhul on suurendus negatiivne, kui objekti kaugus on suurem kui objektiivi fookuskaugus. See ei tähenda, et tekkinud pilt oleks väiksem. Sellisel juhul suureneb ikka, kuid vaatleja näeb moodustatud pilti tagurpidi (ülevalt alla).