Statistikas on vahemik andmekogumi kõrgeima väärtuse ja andmekogumi madalaima väärtuse vahe. Vahemik näitab, kui jagatud väärtused on jadas. Kui vahemik on suur, on seeria väärtused väga hajutatud; kui vahemik on väike, siis seeria väärtused on üksteise lähedal. Kui soovite teada, kuidas katvust arvutada, järgige neid samme.
Samm
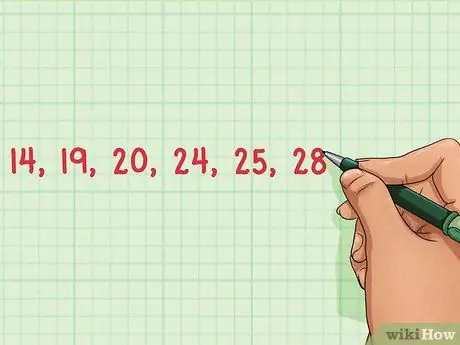
Samm 1. Loetlege oma andmekogumi elemendid
Andmekogumi vahemiku leidmiseks peate loetlema kõik andmekogumi elemendid, et saaksite tuvastada suurimad ja väikseimad numbrid. Kirjutage kõik elemendid üles. Selle andmekogumi numbrid on: 14, 19, 20, 24, 25 ja 28.
- Andmekogumi suurimaid ja väikseimaid numbreid on lihtsam tuvastada, kui tellite numbrid väikseimast suurimani. Selles näites oleks andmekogum üles ehitatud järgmiselt: 14, 19, 20, 24, 24, 25, 28.
- Andmekogumi elementide sorteerimine aitab teil teha ka muid arvutusi, näiteks leida andmekogumi režiimi, keskmist või mediaani.
Samm 2. Tuvastage andmekogumi suurimad ja väikseimad numbrid
Selle probleemi puhul on andmekogumi väikseim arv 14 ja suurim 28.
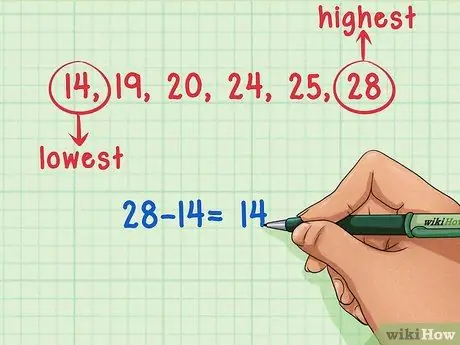
Samm 3. Lahutage suurimast arvust oma andmekogumi väikseim arv
Nüüd, kui olete andmekogumis tuvastanud väikseimad ja suurimad numbrid, peate vaid need üksteisest lahutama. Andmekogumi vahemiku 11 saamiseks lahutage 14 25 -lt (25–14).
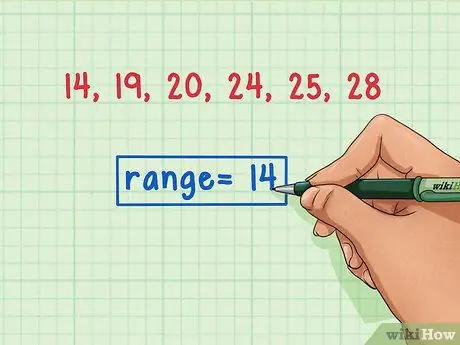
Samm 4. Märgistage vahemik selgelt
Kui olete vahemiku leidnud, märkige see selgelt. See aitab vältida segadust muude statistiliste arvutustega, mida peate tegema, näiteks mediaani, režiimi või keskmise leidmisega.
Näpunäiteid
- Vahemikku saate tõlgendada ka algebraliselt, kuid kõigepealt peate mõistma algebralise funktsiooni mõistet või teadaolevate numbrite toimingute komplekti. Kuna funktsioonitoiminguid saab teha mis tahes numbriga, isegi tundmatu numbriga, tähistatakse numbrit tähtmuutujaga, tavaliselt x -ga. Domeen on võimalike sisendväärtuste kogum, mille saate asendada tundmatu numbriga. Seega on vahemik võimalike arvutustulemuste kogum, mille saate pärast ühe domeeniväärtuse sisestamist ja kõigi funktsiooni määratletud toimingute lõpetamist. Kahjuks pole funktsiooni ulatust võimalik arvutada. Mõnikord võib funktsiooni joonistamine või mitme väärtuse arvutamine näidata selget mustrit. Samuti saate kasutada oma teadmisi funktsiooni domeenist, et kõrvale jätta võimalikud väljundväärtused (arvutustulemused) või kitsendada vahemikku esindavat andmekogumit.
- Iga statistilise andmekogumi mediaanväärtus tähistab andmekogumi mediaanväärtust andmete leviku, mitte vahemiku osas. Ehkki võiksite eeldada, et antud andmekogumi mediaan on vahemik, mis on jagatud 2 -ga või poole vahemikuga, ei ole see tavaliselt tõsi. Õige mediaani leidmiseks peate andmeelemendid sorteerima ja seejärel otsima elementi loendi keskelt. See element on mediaan. Näiteks kui teil on 29 elemendist koosnev loend, on 15. elemendil loendi algusest ja loendi lõpust sama vahemik, seega on 15. element mediaan, olenemata sellest, kuidas selle elemendi väärtus on seotud ulatus.
