- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:13.
- Viimati modifitseeritud 2025-01-23 12:16.
P väärtus on statistiline mõõtmine, mis aitab teadlastel kindlaks teha, kas nende hüpotees on õige. P -väärtust kasutatakse selleks, et teha kindlaks, kas nende katse tulemused jäävad uuritud asjade jaoks tavapäraste väärtuste vahemikku. Tavaliselt, kui andmekogumi P väärtus langeb alla teatud ettemääratud väärtuse (näiteks 0,05), lükkavad teadlased tagasi oma katse nullhüpoteesi - teisisõnu välistavad nad hüpoteesi, kus eksperimentaalsel muutujal on ei mõjuta oluliselt tulemust. Tänapäeval leitakse p väärtused tavaliselt võrdlustabelitest, arvutades chi ruudu väärtuse.
Samm

1. samm. Määrake oma katse oodatavad tulemused
Tavaliselt, kui teadlased teevad katse ja uurivad tulemusi, on neil juba ettekujutus normaalsetest või tavalistest tulemustest. See võib põhineda varasemate katsete tulemustel, usaldusväärsetel vaatlusandmete kogumitel, teaduskirjandusel ja/või muudel allikatel. Katse jaoks määrake oodatav tulemus ja kirjutage see numbrina üles.
Näide: Oletame, et eelmine uuring näitas, et riiklikul tasandil väljastati kiiruseületamise pileteid sagedamini punastele kui sinistele autodele. Oletame, et keskmine tulemus riigi tasandil näitab suhet 2: 1, punaste autode suhtarv on suurem. Soovime teada saada, kas ka meie linna politseil on sama tendents, analüüsides meie linna politsei väljastatud kiiruseületamise piletit. Kui me võtaksime juhusliku valimi 150 kiirusepiletist, mis anti meie linna punastele ja sinistele autodele, siis me ootaksime 100 punase auto jaoks ja 50 siniste autode puhul, kui meie linna politseiüksus annab pileti vastavalt võrdlusele riiklikul tasandil.

Samm 2. Määrake oma eksperimentaalsed tähelepanekud
Nüüd, kui olete oma eeldatava väärtuse kindlaks määranud, saate oma katse käivitada ja leida tegeliku väärtuse (või tähelepaneku). Jällegi kirjutage tulemus numbrina. Kui me manipuleerime mõningate katsetingimustega ja täheldatud tulemused erinevad oodatavatest tulemustest, on kaks võimalust: kas see juhtus juhuslikult või põhjustas selle erinevuse meie manipuleerimine eksperimentaalsete muutujatega. P-väärtuse leidmise eesmärk on põhimõtteliselt kindlaks teha, kas vaadeldavad tulemused erinevad oodatavatest tulemustest punktini, kus nullhüpoteesi-hüpoteesi, et eksperimentaalse muutuja ja vaadeldud tulemuste vahel puudub seos-ei saa tagasi lükata.
Näide: Oletame, et meie linnas valime juhuslikult 150 kiiruseületamise piletit, mis antakse nii punasele kui ka sinisele autole. Saame 90 pilet punasele autole ja 60 sinise auto jaoks. See erineb tulemusest, mida ootasime, st 100 ja 50. Kas meie eksperimentaalne manipuleerimine (antud juhul andmeallika muutmine riiklikust kohalikuks) põhjustas tulemustes muutusi või oli meie linnapolitseil samad tendentsid kui riiklikul tasandil ja me lihtsalt täheldasime kokkusattumust? P väärtus aitab meil seda määrata.

Samm 3. Määrake oma katse vabadusastmed
Vabadusastmed on uuringu varieeruvuse mõõt, mille määrab teie uuritud kategooriate arv. Vabadusastmete võrrand on Vabadusastmed = n-1, kus n on teie katses analüüsitud kategooriate või muutujate arv.
-
Näide. Meie katses on kaks tulemuste kategooriat: üks punase ja teine sinise auto jaoks. Seega on meie katses 2-1 = 1 vabadusaste.
Kui võrrelda punaseid, siniseid ja rohelisi autosid, siis saame
2. samm. vabadusastmed ja nii edasi.

Samm 4. Võrrelge oodatud tulemusi vaadeldud tulemustega, kasutades chi ruutu
Chi ruut (kirjutatud x2) on arvväärtus, mis mõõdab katse oodatud ja täheldatud väärtuste erinevust. Chi ruudu võrrand on järgmine: x2 = ((o-e)2/e), kus o on vaadeldav väärtus ja e on eeldatav väärtus. Lisage selle võrrandi tulemused kõigi võimalike tulemuste kohta (vt allpool).
- Pange tähele, et see võrrand kasutab operaatorit (sigma). Teisisõnu, peate arvutama ((| o-e | -.05)2/e) iga võimaliku tulemuse kohta, siis liida tulemused kokku, et saada chi ruudu väärtus. Meie näites on meil kaks tulemust - auto, mis saab punase või sinise pileti. Seega saame arvutada ((o-e)2/e) kaks korda - üks kord punase ja üks kord sinise auto jaoks.
-
Näide: ühendame oma eeldatavad väärtused ja tähelepanekud võrrandisse x2 = ((o-e)2/e). Pidage meeles, et sigmaoperaatori tõttu peame arvutama ((o-e)2/e) kaks korda - üks kord punase ja üks kord sinise auto jaoks. Töötlemisetapid on järgmised:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Samm 5. Valige olulisuse tase
Nüüd, kui me teame oma eksperimentaalse komplekti vabadusastmeid ja chi ruudu väärtust, peame enne p-väärtuse leidmist tegema vaid ühe viimase asja-peame määrama olulisuse taseme. Põhimõtteliselt on olulisuse tase mõõtmine selle kohta, kui kindlad oleme oma tulemustes - madal olulisuse tase vastab madalale tõenäosusele, et katse tulemus oli tingitud juhusest ja vastupidi. Olulisuse tase kirjutatakse kümnendkohana (nt 0,01), mis vastab protsendilisele tõenäosusele, et katse tulemus oli tingitud juhusest (antud juhul 1%).
- Kokkuleppe kohaselt määravad teadlased tavaliselt oma eksperimentide olulisuse väärtuseks 0,05 või 5 protsenti. See tähendab, et sellele olulisuse tasemele vastavatel katsetulemustel on kokkulangevuse tõenäosus maksimaalselt 5%. Teisisõnu on 95% tõenäosus, et tulemused on tingitud teadlase manipuleerimisest eksperimentaalsete muutujatega, mitte juhusest. Enamiku katsete puhul peetakse 95% usaldust kahe muutuja vahelise seose kohta nende kahe vahelise seose demonstreerimiseks edukaks.
- Näide: meie punase ja sinise auto näite puhul lähtume teaduslikust kokkuleppest ja määrame oma olulisuse taseme 0, 05.
Samm 6. Kasutage chi ruutjaotustabelit oma p-väärtuse hindamiseks
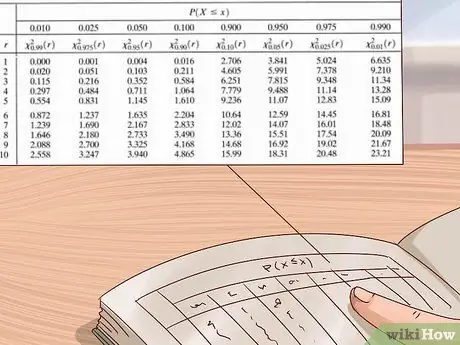
Teadlased ja statistikud kasutavad oma katsete p väärtuste arvutamiseks suuri väärtustabeleid. See tabel on tavaliselt kirjutatud nii, et vertikaaltelg vasakul näitab vabadusastmeid ja üleval olev horisontaaltelg näitab p-väärtusi. Kasutage seda tabelit, leidke esmalt oma vabadusastmed, seejärel lugege ridu vasakult paremale, kuni leiate esimese väärtuse, mis on suurem kui teie chi ruut. Vaadake p-väärtust veeru ülaosas-teie p-väärtus jääb selle väärtuse ja järgmise suurima väärtuse vahele (parem väärtus on sellest vasakul).
- Chi ruutjaotustabelid on saadaval erinevatest allikatest - need on hõlpsasti leitavad veebist või teaduse või statistika õpikutest. Kui teil seda pole, kasutage ülaltoodud fotol näidatud tabelit või tasuta veebilauda, näiteks seda, mille pakub siin medcalc.org.
-
Näide: meie chi ruut on 3. Seega kasutame ligikaudse p-väärtuse leidmiseks ülaltoodud fotol olevat chi ruutjaotustabelit. Kuna me teame, et meie katses on ainult
Samm 1. vabadusastmeid, alustame ülemisest tabelist. Selles reas liigume vasakult paremale, kuni leiame väärtuse, mis on suurem kui
3. samm. - meie chi ruudu väärtus. Esimene leitud väärtus on 3,84. Seda veergu otsides näeme, et vastav p-väärtus on 0,05. See tähendab, et meie p-väärtus on vahemikus 0,05 kuni 0,1 (tabeli suuruselt järgmine p-väärtus).

Samm 7. Otsustage, kas lükata tagasi või kaitsta oma nullhüpoteesi
Kuna olete oma eksperimendi jaoks leidnud ligikaudse p-väärtuse, saate otsustada, kas lükkate oma katse nullhüpoteesi tagasi (meeldetuletuseks, see on hüpotees, et teie manipuleeritud eksperimentaalne muutuja ei mõjutanud teie täheldatud tulemusi). Kui teie p-väärtus on teie olulisuse väärtusest madalam, õnnitleme-olete tõestanud, et on suur tõenäosus, et teie manipuleeritud muutujate ja teie tähelepanekute vahel on seos. Kui teie p-väärtus on suurem kui teie olulisuse väärtus, ei saa te kindlalt väita, et teie jälgitavad tulemused on pelga juhuse või katsega manipuleerimise tulemus.
- Näide: meie p-väärtus on vahemikus 0,05 kuni 0,1. See tähendab, et see pole sugugi väiksem kui 0,05, seega kahjuks ei saa meie nullhüpoteesi tagasi lükata. See tähendab, et me ei saavuta minimaalset 95% usalduspiiri, mille oleme seadnud, et saaks öelda, et meie linna politsei annab piletipileteid punastele ja sinistele autodele vahekorras, mis on riigi keskmisest üsna erinev.
- Teisisõnu on 5-10% tõenäosus, et meie tähelepanekud ei tulene asukoha muutusest (analüüsides meie linna ja mitte kogu osa), vaid on juhused. Kuna me otsime tõenäosust alla 5%, ei saa me seda öelda veendunud et meie linna politsei kipub piletitega punaseid autosid ostma - on väike, kuid statistiliselt väga erinev võimalus, et neil seda tendentsi pole.
Näpunäiteid
- Teaduslik kalkulaator teeb arvutused palju lihtsamaks. Kalkulaatoreid saate otsida ka Internetist.
- P-väärtusi saate arvutada mitmete arvutiprogrammide, sealhulgas tavaliselt kasutatava arvutustabelitarkvara ja spetsiaalsema statistikatarkvara abil.






